重要なクラス - Random

Random クラスは、一般的に必要とされる様々な種類の乱数値を簡単に生成する方法を提供します。

このページでは、Random クラスの概要と、Random クラスを使ってスクリプトを作成する際の一般的な使い方について説明します。Random クラスのすべてのメンバーの詳細なリファレンスや、技術的な詳細については、Random スクリプトリファレンス を参照してください。

これらの便利な方法の詳細や例については、後述のリンクを参照してください。

単純な乱数

Random.value gives you a random floating point number between 0.0 and 1.0. A common usage is to convert it to a number between zero and a range of your choosing by multiplying the result.

Random.Range gives you a random number between a minimum and maximum value that you provide. It returns either an integer or a float, depending on whether the the min and max values provide are integers or floats.

円または球体内のランダムな点

Random.insideUnitCircle returns a randomly selected point inside a circle with a radius of 1 (Again you can multiply the result to get a random point within a circle of any size).

Random.insideUnitSphere returns a randomly selected point inside a sphere with a radius of 1.

Random.onUnitSphere returns a randomly selected point on the surface of a sphere with a radius of 1.

その他の種類の乱数値

Unity の Random クラスには、他にもいくつかのランダム値の種類があります。

To generate a random rotation, use Random.rotation.

ランダムな 色 を生成するには、Random.ColorHSV を使用します。

配列からのランダムな選択

ランダムな配列要素を選ぶことはランダムな整数を 0 から配列の最大のインデックス値（配列の長さから 1 を引いた値）を選ぶことに要約できる。これは内蔵の Random.Range 関数により実現できます。

 var element = myArray[Random.Range(0, myArray.Length)];

Random.Range が最初の引数の含むけれども二つめの引数は除かれるため、myArray.Length とすることが正しいことに注意してください。

確率の異なるアイテムの選択

アイテムをランダムに選択する場合に、あるアイテムの選択確率を他よりも高くしたい場合があります。例えば、NPC キャラクターがプレイヤーに遭遇するときに、いくつかの異なる反応を示すとします。

• 50% の確率で挨拶する
• 25% の確率で逃げだす
• 20% の確率で急に攻撃する
• 5% 確率でお金をプレゼント

これらの異なる結果を分割した紙切れで表現することができて、おのおのの切れ端は紙切れの全長の一部を占めるとします。その占める長さが選択される結果の確率に相当します。選択を行うことは紙切れの長さ上の任意の点を選んで（例えばダーツを投げるように）、どの切れ端にあたるか確認することに相当します

スクリプトの中では紙切れは実際には float の配列で、おのおののアイテムに異なる確率を順に格納しています。ランダムな点は Random.value をすべての float の合計に掛け算することで得られます（足して 1 になる必要はなく、重要なことは異なる値の相対的な長さ）。点がどの配列要素に “入っているか” 調べるために、点の値が最初の要素の値より小さいか比較します。それであれば選択されるのは最初の要素です。そうでなければ、最初の要素の値を点の値から引き算して、それを二つめの要素の値より小さいか比較する、などを繰り返して最終的に正しい要素を見つけます。コードでは次のようになるはずです。

float Choose (float[] probs) {

    float total = 0;

    foreach (float elem in probs) {
        total += elem;
    }

    float randomPoint = Random.value * total;

    for (int i= 0; i < probs.Length; i++) {
        if (randomPoint < probs[i]) {
            return i;
        }
        else {
            randomPoint -= probs[i];
        }
    }
    return probs.Length - 1;
}

Random.value は 1 の値を返す可能性があるため、最後の return ステートメントが必要であるということに注意してください。このケースでは、検索はランダムな点をどこにも見つけることができません。次の行を変更して、

 if (randomPoint < probs[i])

… 値を <= 記号に変更することで余分な return ステートメントを回避できますが、確率が 0 の場合でもアイテムを選択することも許容してしまいます。

連続的なランダム数の重み付け

個別の結果を持っている場合、float 配列の手法は上手く動作しますが、より連続的な結果を生成したい状況もあります。すなわち、宝箱で見つかった金貨の枚数をランダム化したいときや 1 - 100 の範囲のランダム値でもより低い値を取得する可能性が高いことを望む場合です。これを行うには float 配列の手法を使用すると、100 つの float から成る配列を作る必要があり (例えば、細長い紙の分割のように) 面倒です。また、整数に限らず範囲内のすべての数が必要な場合は、そのアプローチを使うことは不可能です。

連続した結果に対するよりよいアプローチとして、ランダムな値 ‘raw’ を ‘weighted’ なものに変換するのに AnimationCurve を使用することです。違うカーブの形状を描画することで、異なる重み付けを生成することができます。コードも書くのはもっと簡単です。

float CurveWeightedRandom(AnimationCurve curve) {
    return curve.Evaluate(Random.value);
}

0 と 1 の間のランダムな値 raw は、Random.value から読み込むことで選択されます。次に、水平座標としてそれを処理する curve.Evaluate() に渡され、水平位置でカーブに対応する垂直座標を返します。カーブの浅い部分は選択される大きなチャンスがある一方、急な部分は選択されるチャンスが少ないです。

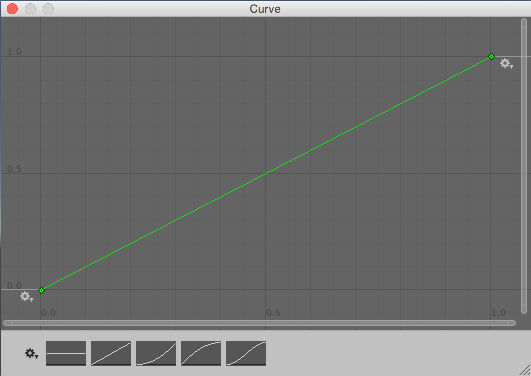
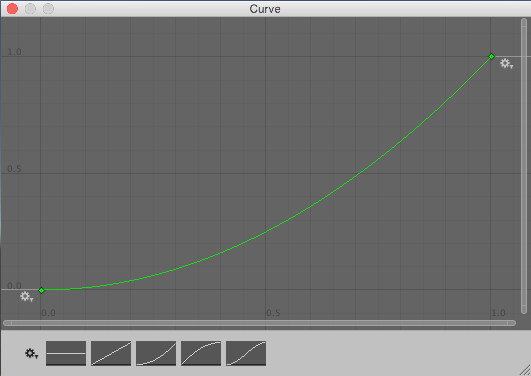
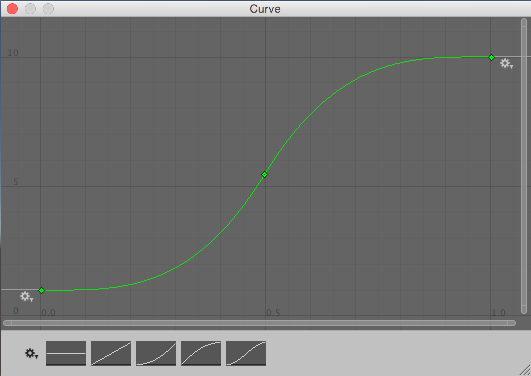
これらのカーブは、確率論のガイドで見つかるかもしれないような確立分布曲線ではなく、もっと逆累積分布曲線のようであると気付いてください。

複数あるスクリプトのうち1つにパブリックの Animation Curve 変数を定義することにより、値を計算する必要性に代わって、視覚的に Inspector ウィンドウを通してカーブを見て編集することができます。

このテクニックは浮動小数点を生成します。整数の結果を計算したい場合、例えば、82.1214 金貨ではなく82 金貨を望むときは Mathf.RoundToInt() のような関数に対して単に計算された値を渡すことができます。

リストのシャッフル

よくあるゲームシステムに、既に決まったアイテム群からランダムな順番で選択するというものがあります。例えば、カードの山は一般的にはシャッフルして予想できる順番にならないようにします。各要素を他のランダムな配列インデックスの要素と入れ替えることによって、配列のアイテムをシャッフルできます。

void Shuffle (int[] deck) {
    for (int i = 0; i < deck.Length; i++) {
        int temp = deck[i];
        int randomIndex = Random.Range(0, deck.Length);
        deck[i] = deck[randomIndex];
        deck[randomIndex] = temp;
    }
}

アイテム群から繰り返しなしに選択

同じものを何度も選択することなしに、アイテム群から複数のアイテムをランダムに選択する、という作業があります。例えば、ランダムな生成地点で複数の NPC を生成したいが、各地点において 1 つの NPC のみを生成したい場合があります。これは、アイテムを順番に繰り返し、選択したアイテム群に追加するかどうかをランダムに決定することで実行できます。 各アイテムを順番にチェックするので、そのアイテムが選択される確率は、まだ必要なアイテムの数を、まだ選択可能な残りのアイテム数で割ったものに等しくなります。

例として、10 つの使用可能な生成地点から、5 つだけを選択する必要があるとします。最初のアイテムが選択される確率は、5/10 または 0.5 になります。それが選択されると、2 番目のアイテムの確率は 4/9 または 0.44 になります (つまり、4 つのアイテムがまだ必要で、残りの 9 つから選択できます)。ただし、最初のものが選択されなかった場合、2 番目の確率は 5/9 または 0.56 になります (つまり、5 つがまだ必要で、残りの 9 つから選択できます)。これは、必要な 5 つのアイテムが選択されるまで続きます。次のコードで行えます。

Transform[] spawnPoints;

Transform[] ChooseSet (int numRequired) {
    Transform[] result = new Transform[numRequired];

    int numToChoose = numRequired;

    for (int numLeft = spawnPoints.Length; numLeft > 0; numLeft--) {

        float prob = (float)numToChoose/(float)numLeft;

        if (Random.value <= prob) {
            numToChoose--;
            result[numToChoose] = spawnPoints[numLeft - 1];

            if (numToChoose == 0) {
                break;
            }
        }
    }
    return result;
}

選択がランダムであるにも関わらず、選択されたアイテム群は元の配列と同じ順序であることに注意してください。アイテムを 1 度に 1 つずつ順番に使用する場合は、順序は部分的に予測可能であるため、使用する前に配列をシャッフルする必要があるかもしれません。

空間上のランダムな点

立方体の体積におけるランダムな点は、Vector3 の各々のコンポーネントを Random.value により返される値でセットすることで選択できます :

 var randVec = Vector3(Random.value, Random.value, Random.value);

これにより辺の長さが 1 単位である立方体の中の点が返されます。立方体を拡大/縮小するにははベクトルの X、Y、Z 要素を希望する辺の長さに掛け算するのみです。もし軸のひとつが 0 にセットされる点はひとつの平面上に置かれます。例えば、ランダムな地点を “地面” から選ぶ必要がある場合は、X、Z をランダムに選択して、Y は 0 にセットすることになります。

体積が球である場合（すなわち、原点から一定の半径に含まれるランダムな点が必要な場合）、Random.insideUnitSphere を希望の半径に掛け算できます:

 var randWithinRadius = Random.insideUnitSphere * radius;

もし結果のベクトルの要素のひとつを 0 にしても、円の中のランダムな点を正しく得ることには「できません」。点は確かにランダムで、半径は希望する範囲内にありますが、確率が円周に近づくにつれ大きく偏りができていて、点は不均等に並びます。その状況では変わりに Random.insideUnitCircle を使用すべきです:

 var randWithinCircle = Random.insideUnitCircle * radius;