Понимание векторной арифметики

Векторная арифметика - основа 3D графики, физики и анимации, и, для получения максимальной отдачи от Unity, весьма полезно досконально разбираться в этой теме. Ниже приведены описания основных операций и несколько советов о том, для чего они могут быть использованы.

Сложение

При сложении 2 векторов результат эквивалентен тому, что получится если исходные векторы принять за следующие друг за другом “шаги”. Заметьте, что порядок двух слагаемых не важен, т.к. в любом случае результат будет одинаковый.

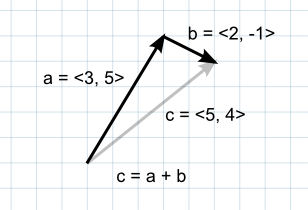
Если первый вектор принять за точку в пространстве, то второй вектор можно интерпретировать как сдвиг или “прыжок” из этой точки. Например, чтобы для поиска точки 5-тью единицами выше точки на земле, вы могли бы использовать следующий расчёт:-

 var pointInAir = pointOnGround + new Vector3(0, 5, 0);

Если векторы представляют собой силы, то более естественно будет думать о них с точки зрения их направления и величины (величина определяет мощность силы). Сложение двух векторов силы в результате даёт новый вектор, эквивалентный комбинации этих сил. Этот концепт зачастую очень полезен при применении сил с различными раздельными компонентами, которые работают одновременно (например, на летящую вперёд ракету может влиять встречный или боковой ветер).

Вычитание

Вычитание векторов чаще всего используется, чтобы узнать расстояние и направление одного объекта относительно другого. Заметьте, что при вычитании порядок параметров имеет значение:-

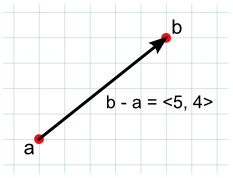
// The vector d has the same magnitude as c but points in the opposite direction.
var c = b - a;
var d = a - b;

Как и с обычными числами, прибавление отрицательного вектора - это то же самое, что и вычитание положительного.

// These both give the same result.
var c = a - b;
var c = a + -b;

Отрицательный вектор имеет ту же величину, что и исходный вектор, и лежит на той же прямой, только в обратном направлении.

Скалярные умножение и деление

Говоря о векторах, в порядке вещей обращаться к обычным числам (например, значениям типа float) как к скалярам. Это значит, что у них есть только “размер” или величина, в то время как у векторов есть и величина и направление.

Умножение вектора на скаляр даёт в результате вектор, с тем же направлением, что и исходный вектор. Тем не менее, величина нового вектора равна исходной величине умноженной на скалярное значение.

Аналогично, скалярное деление делит исходную величину вектора на скаляр.

Эти операции полезны, когда вектор представляет из себя смещение движения или силу. Они позволяют вам изменить величину вектора без влияния на его направление.

Когда любой вектор делится на собственную величину, то в результате получается вектор величиной 1, известный как нормированный (единичный) вектор. Если нормированный вектор умножить на скаляр, то величина результата будет равна значению скаляра. Это полезно, когда направление силы постоянно, а величина - нет (например, сила от колеса автомобиля всегда толкает вперёд, но её мощность контролируется водителем).

Скалярное произведение (Dot Product)

Скалярное произведение получает 2 вектора и возвращает скаляр. Этот скаляр равен произведению величин этих векторов, умноженному на косинус угла между ними. Когда оба вектора - нормированные, косинус по сути дела утверждает, как далеко первый вектор простирается в направлении второго (или наоборот - порядок параметров роли не играет).

Если работать с точки зрения углов, то можно достаточно просто найти соответствующие косинусы используя калькулятор. Тем не менее, полезно иметь интуитивное понимание основных значений косинуса, как показано на диаграмме ниже:-

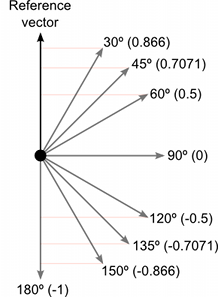
Скалярное произведение - это очень простая операция, которую, при некоторых обстоятельствах, можно использовать вместо функции Mathf.Cos или операции векторных величин (оно не делает в точности то же самое, но иногда эффект получается одинаковый). Тем не менее, вычисление скалярного произведения на уровне процессора проходит значительно быстрее, так что оно может оказаться ценной оптимизацией.

Векторное произведение (Cross Product)

Другие операции предназначены для 2D или 3D векторов и для действительных векторов с любым числом измерений. Векторное произведение же, напротив, имеет смысл применять только для 3D векторов. Оно использует 2 вектора как входную информацию и возвращает ещё один вектор в качестве результата.

Итоговый вектор перпендикулярен двум исходным векторам. Можно использовать “правило левой руки”, чтобы запомнить направление выходного вектора относительно исходных векторов. Если первый параметр совпадает с большим пальцем руки, а второй параметр с указательным пальцем, то результат будет указывать в направлении среднего пальца. Если использовать обратный порядок параметров, то тогда итоговый вектор будет указывать в противоположном направлении, но его величина не изменится.

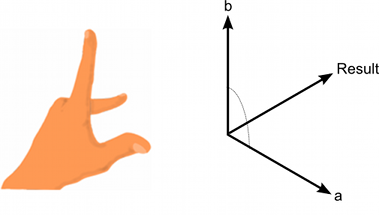
Величина результата равна произведению величин исходных векторов, умноженному на синус угла между ними. Некоторые полезные значения функции синуса указаны ниже:-

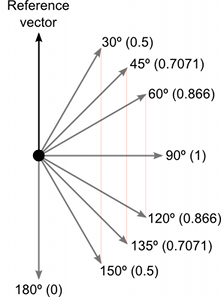
Векторное произведение может выглядеть сложным, т.к. оно включает в себя сразу несколько полезных частей информации в возвращённой величине. Тем не менее, как и скалярное произведение, оно очень эффективно с математической точки зрения и может быть использовано для оптимизации кода, который иначе будет зависеть от медленных и сложных функций.