Important Classes - Vectors

Vectors are a fundamental mathmatical concept which allow you to describe a direction and magnitude. In games and apps, vectors are often used describe some of the fundamental properties such as the position of a character, the speed something is moving, or the distance between two objects.

Vector arithmetic is fundamental to many aspects of computer programming such as graphics, physics and animation, and it is useful to understand it in depth to get the most out of Unity.

Vectors can be expressed in multiple dimensions, and Unity provides the Vector2, Vector3 and Vector4 classes for working with 2D, 3D, and 4D vectors. These three types of Vector classes all share many of the same functions, such as magnitude, so most of the information on this page applies to all three types of Vector unless otherwise specified.

This page provides an overview of the Vector classes and their common uses when scripting with them. For an exhaustive reference of every member of the vector classes, see the script reference pages for Vector2, Vector3 and Vector4.

Understanding Vector Arithmetic

Addition

Cuando dos vectores son agregados juntos, el resultado es equivalente a tomar los vectores originales como “pasos”, uno después del otro. Tenga en cuenta que el orden de los dos parámetros no importa, ya que el resultado es el mismo de la misma manera.

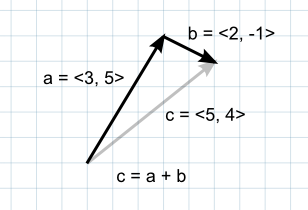
Si el primer vector es tomado como un punto en el espacio, entonces el segundo puede ser interpretado como el desplazamiento o “salto” desde esa posición. Por ejemplo, para encontrar un punto 5 unidades encima de una ubicación en el suelo, usted puede utilizar el siguiente cálculo:-

 var pointInAir = pointOnGround + new Vector2(0, 5);

Si los vectores representan fuerzas, entonces es más intuitivo pensar en ellos en términos de su dirección y magnitud (la magnitud indica el tamaño de la fuerza). Agregar dos vectores de fuerza resulta en nuevo vector equivalente a la combinación de las fuerza. Este concepto suele ser útil cuándo se aplique fuerzas con varios componentes actuando una vez (eg, un cohete siendo propulsado hacia al frente puede también ser afectado por un viento cruzado).

Although the examples here show 2D vectors, the same concept applies to 3D and 4D vectors.

Subtraction

La resta de Vectores se utiliza con mayor frecuencia para obtener la dirección y distancia de un objeto a otro. Tenga en cuenta que el orden de los dos parámetros sí importa con la substracción:-

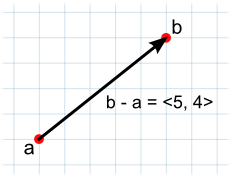
// .El vector d tiene la misma magnitud que c pero apunta en la dirección opuesta
var c = b - a;
var d = a - b;

Como con los número, agregando el negativo de un vector es lo mismo que restar el positivo.

// Ambos dan el mismo resultado.
var c = a - b;
var c = a + -b;

El negativo de un vector tiene la misma magnitud como el original y apunta a lo largo de la misma linea pero exactamente en la posición opuesta.

Direction and Distance from One Object to Another

Si un punto en el espacio es restado de otro entonces el resultado es un vector que “apunta” de un objeto al otro.

// Obtiene un vector que apunta desde la posición del jugador a la del objetivo.
var heading = target.position - player.position;

As well as pointing in the direction of the target object, this vector’s magnitude is equal to the distance between the two positions. You may need a “normalized” vector giving the direction to the target, but with a fixed distance (say for directing a projectile). You can normalize a vector by dividing it by its own magnitude:

var distance = heading.magnitude;
var direction = heading / distance; // This is now the normalized direction.

Este acercamiento es preferible para utilizar ambas propiedades de magnitud y normales separadamente, ya que ambas son bastante “hambrientas” en CPU (ambas involucran calcular una raíz cuadrada).

Si usted solo necesita utilizar la distancia para comparación (para una revisión aproximada, digamos) entonces usted puede evitar los cálculos de magnitud todo juntos. La propiedad sqrMagnitud da el cuadrado del valor de la magnitud, y está calculado como la magnitud pero sin la operación que toma tiempo de la raíz cuadrada. En vez de comparar la magnitud contra una distancia conocida, usted puede compara la magnitud cuadrada contra la distancia cuadrada:-

if (heading.sqrMagnitude < maxRange * maxRange) {
    // Target is within range.
}

Esto es más eficiente que utilizar magnitud verdadera en la comparación.

Sometimes, when working in 3D, you might need an “overground heading” to a target. For example, imagine a player standing on the ground who needs to approach a target floating in the air. If you subtract the player’s position from the target’s then the resulting vector will point upwards towards the target. This is not suitable for orienting the player’s transform since they will also point upwards; what is really needed is a vector from the player’s position to the position on the ground directly below the target. You can obtain this by taking the result of the subtraction and setting the Y coordinate to zero:-

var heading = target.position - player.position;
heading.y = 0;  // This is the overground heading

Scalar Multiplication and Division

Cuando discutan vectores, es común referirse a un número ordinario (eg, un valor float) como escalar. El significado de esto es que un escalar solo tiene una “escala” o una magnitud dónde un vector tiene ambas magnitud y dirección.

Multiplicar un vector por un escalar resulta en un vector que apunta en la misma dirección como el original. No obstante, la nueva magnitud del vector es igual a la magnitud original multiplicado por el valor escalar.

Del mismo modo, la división escalar divide la magnitud del vector original por el escalar.

Estas operaciones son útiles cuándo el vector representa el desplazamiento de un movimiento o una fuerza. Ellas le permiten a usted cambiar la magnitud del vector sin afectar su dirección.

Cuando cualquier vector es dividido por su propia magnitud, el resultado es un vector con una magnitud de 1, que es conocido como un vector normalizado. Si un vector normalizado es multiplicado por un escalar entonces la magnitud del resultado va a ser igual al valor del escalar. Esto es útil cuándo la dirección de una fuerza es constante pero la fuerza es controlable (eg, la fuerza de la llanta de un carro siempre empuja hacia el frente pero el poder es controlado por el conductor).

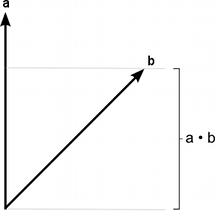
Dot Product

El producto punto toma dos vectores y devuelve un escalar. Este escalar es igual a las magnitudes de dos vectores multiplicados juntos y el resultado es multiplicado por el coseno del ángulo entre los vectores. Cuando los dos vectores son normalizados, el coseno esencialmente declara qué tan lejos el primer vector se extiende en la dirección del segundo (o vice-versa - el orden de los parámetros no importa).

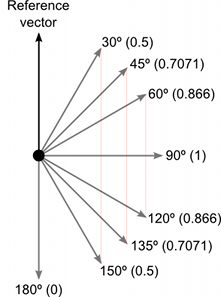
Below you can see a comparison of how vectors of varying angles compared with a reference vector return a dot product value between 1 and –1 :

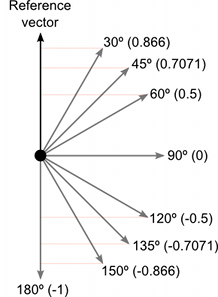
The dot product is a mathematically simpler operation than calculating the cosine, so it can be used in place of the Mathf.Cos function or the vector magnitude operation in some circumstances (it doesn’t do exactly the same thing but sometimes the effect is equivalent). However, calculating the dot product function takes much less CPU time and so it can be a valuable optimization.

The dot product is useful if you want to calculate the amount of one vector’s magnitude that lies in the direction of another vector.

For example, a car’s speedometer typically works by measuring the rotational speed of the wheels. The car may not be moving directly forward (it may be skidding sideways, for example) in which case part of the motion will not be in the direction the car is facing - and so won’t be measured by the speedometer. The magnitude of an object’s rigidbody.velocity vector will give the speed in its direction of overall motion but to isolate the speed in the forward direction, you should use the dot product:

var fwdSpeed = Vector3.Dot(rigidbody.velocity, transform.forward);

Naturalmente, la dirección puede ser lo que uno quiera, pero la dirección del vector siempre debe estar normalizada para este cálculo. No sólo el resultado es más correcto que la magnitud de la velocidad, sino que también evita la lenta operación de obtener la raíz cuadrada para encontrar la magnitud.

Cross Product

The cross product is only meaningful for 3D vectors. It takes two 3D vectors as input and returns another 3D vector as its result.

The result vector is perpendicular to the two input vectors. You can use the “left hand rule” to remember the direction of the output vector from the ordering of the input vectors. If the first parameter is matched up to the thumb of the hand and the second parameter to the forefinger, then the result will point in the direction of the middle finger. If the order of the parameters is reversed then the resulting vector will point in the exact opposite direction but will have the same magnitude.

La magnitud del resultado es igual a las magnitudes de los vectores input multiplicados juntos y luego ese valor multiplicado por el seno del ángulo entre ellos. Algunos valores útiles de la función seno son mostrados abajo:-

The cross product can seem complicated since it combines several useful pieces of information in its return value. However, like the dot product, it is very efficient mathematically and can be used to optimize code that would otherwise depend on slower transcendental functions such as sine and cosine.

Computing a Normal/Perpendicular vector

A “normal” vector (ie. a vector perpendicular to a plane) is required frequently during mesh generation and is also useful in path following and other situations. Given three points in the plane, say the corner points of a mesh triangle, you can find the normal as follows: - Pick one of the three points - Subtract it from each of the two other points separately (resulting in two new vectors, “Side 1” and “Side 2”) - Calculate the cross product of the vectors “Side 1” and “Side 2” - The result of the cross product is a new vector that is perpendicular to the plane the three original points lie on - the “normal”.

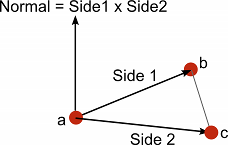
Vector3 a;
Vector3 b;
Vector3 c;

Vector3 side1 = b - a;
Vector3 side2 = c - a;

Vector3 normal = Vector3.Cross(side1, side2);

The “left hand rule” can be used to decide the order in which the two vectors should be passed to the cross product function. As you look down at the top side of the surface (from which the normal will point outwards) the first vector should sweep around clockwise to the second:

El resultado va a apuntar en exactamente la dirección opuesta si el orden de los vectores input se invierten.

Para meshes, el vector de la normal debe también ser normalizado. Esto puede ser hecho con la propiedad normalized, pero hay otro truco que es ocasionalmente útil. Usted puede también normalizar el vector perpendicular dividiéndolo por su magnitud:-

float perpLength = perp.magnitude;
perp /= perpLength;

Another useful note is that the area of the triangle is equal to perpLength / 2. This is useful if you need to find the surface area of the whole mesh or want to choose triangles randomly with probability based on their relative areas.