了解矢量算术
矢量算术是 3D 图形、物理和动画的基础，深入了解这一主题对于充分发挥 Unity 的功能很有帮助。以下是主要运算的说明以及有关它们的用途的一些建议。
添加
当两个矢量相加时，结果相当于将原始矢量依次作为“步骤”。请注意，两个参数的顺序无关紧要，因为两种方式的结果都相同。
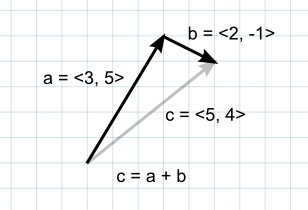
如果将第一个矢量视为空间中的一个点，那么第二个矢量可以解释为从该位置的偏移或“跳跃”。例如，为了找到地面上某个位置上方 5 个单位的点，可使用以下计算：
var pointInAir = pointOnGround + new Vector3(0, 5, 0);
如果矢量代表力，那么从力的方向和大小来考虑它们将会更直观。两个力矢量相加会产生一个等于力的组合的新矢量。施加的力同时有若干单独分量起作用时（例如，向前推进的火箭还可能受到侧风影响），此概念通常很有用。
减法
矢量减法通常用于获取从一个对象到另一个对象的方向和距离。请注意，两个参数的顺序对于减法很__重要__：
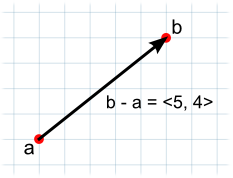
// 矢量 d 的大小与 c 相同，但指向相反的方向。
var c = b - a;
var d = a - b;
与数字一样，与负向矢量相加相当于减去正向矢量。
// 这两者得出相同的结果。
var c = a - b;
var c = a + -b;
负向矢量的大小与原始矢量相同并沿着同一条线指向，但在完全相反的方向上。
标量乘法和除法
在讨论矢量时，通常将普通数（例如，浮点值）称为标量。这意味着标量只有“标度”或大小，而矢量兼具大小和方向。
将矢量乘以标量会产生与原始矢量方向相同的矢量。但是，新矢量的大小等于原始大小乘以标量值。
同样，标量除法将原始矢量的大小除以标量。
当矢量表示移动偏移或力时，这些运算很有用。通过这些运算可以更改矢量的大小而不影响其方向。
当任何矢量除以其自身的大小时，得到的结果是大小为 1 的矢量，即所谓的归一化矢量。如果归一化矢量乘以标量，则结果的大小将等于该标量值。当力的方向恒定但强度可控时（例如，来自车轮的力总是向前推动，但是动力由驾驶员控制），这会很有用。
点积
点积取两个矢量并返回标量。该标量等于两个矢量相乘的大小，得到的结果再乘以矢量之间角度的余弦。当两个矢量都被归一化时，余弦本质上表示第一个矢量在第二个矢量的方向上延伸的距离（反之亦然 - 参数的顺序无关紧要）。
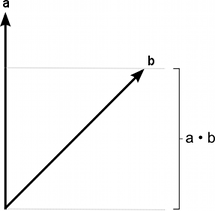
想象成角度再使用计算器找到相应的余弦，这种处理方式比较容易。但是，还有一种有用的方法可以直观了解一些主余弦值，如下图所示：
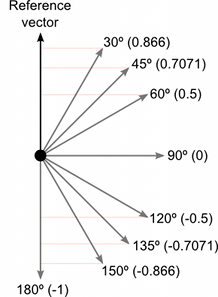
点积是一种非常简单的运算，在某些情况下可用于代替 Mathf.Cos 函数或矢量大小运算（功能不完全相同但有时效果相同）。但是，计算点积函数所需的 CPU 时间要少得多，因此可作为一种有价值的优化。
差积
其他运算是针对 2D 和 3D 矢量甚至任意维度的矢量定义的。相比之下，差积仅对 3D 矢量有意义。它需要两个矢量作为输入，并返回另一个矢量作为结果。
结果矢量垂直于两个输入向量。可使用“左手规则”根据输入矢量的排序确定输出矢量的方向。如果第一个参数对应于手的拇指，而第二个参数对应于食指，则结果将指向中指的方向。如果参数的顺序颠倒，得到的矢量将指向完全相反的方向，但大小相同。
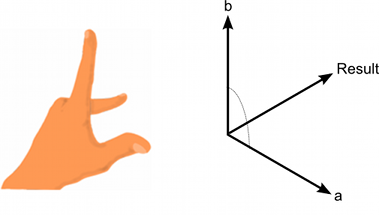
结果的大小等于输入矢量的大小相乘，然后该值再乘以二者之间角度的正弦。正弦函数的一些有用值如下所示：
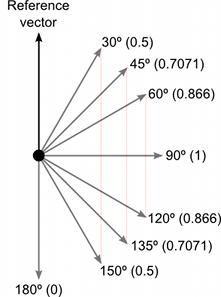
差积看起来很复杂，因为它在返回值中结合了多方面的有用信息。然而，就像点积一样，它在数学上的效率非常高，可用于优化代码，否则这些代码将不得不依赖于缓慢的超越函数。